


Next: About this document ...
C.R. Acad. Sci. Paris
Problèmes mathématiques de la mécanique/Mathematical
problems in Mechanics
(Analyse mathématique/Mathematical analysis)
Dual free boundaries for Stokes waves
Boris BUFFONIa, John Francis TOLANDb
a Département de Mathématiques, Ecole Polytechnique
Fédérale de
Lausanne, CH-1015 Lausanne
b Department of Mathematical Sciences, University of
Bath, Bath BA2 7AY, UK
Courriel:
Boris.Buffoni@epfl.ch,
jft@maths.bath.ac.uk
| Abstract. |
Classically, gravity waves on the surface of a two-dimensional layer of
perfect
fluid are described in potential theory by a free-boundary
problem for the (harmonic) stream function 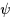 on an unknown domain on an unknown domain 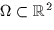 .Many authors independently have transformed this problem by a
conformal mapping into a quasi-linear equation (W)
for a function w of a
single variable. Equation (W) is non-local, as it involves the Hilbert
transform, and it has variational structure, being an Euler-Lagrange
equation.
Here we deal with periodic waves in which case w is periodic.
Our aim is to introduce a new
non-local variational equation (V)
to be satisfied by another periodic function v. The connection
between (V) and (W) is one of duality, in three related senses.
First, there is a system of partial
differential equations with variational structure for a
vector-function .Many authors independently have transformed this problem by a
conformal mapping into a quasi-linear equation (W)
for a function w of a
single variable. Equation (W) is non-local, as it involves the Hilbert
transform, and it has variational structure, being an Euler-Lagrange
equation.
Here we deal with periodic waves in which case w is periodic.
Our aim is to introduce a new
non-local variational equation (V)
to be satisfied by another periodic function v. The connection
between (V) and (W) is one of duality, in three related senses.
First, there is a system of partial
differential equations with variational structure for a
vector-function
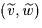 on the unit disc.
Solving this system partially yields either on the unit disc.
Solving this system partially yields either
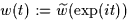 , a solution of (W), or , a solution of (W), or
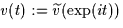 , a solution of (V).
Second, the duality can be defined in terms of a Riemann-Hilbert
problem on the unit circle (RH). Third, there is a direct
relation between the variational principles for (V) and (W).
Most significantly, there is a potential-theoretic problem
corresponding to v. It is also a free-boundary problem for a
(different) harmonic function , a solution of (V).
Second, the duality can be defined in terms of a Riemann-Hilbert
problem on the unit circle (RH). Third, there is a direct
relation between the variational principles for (V) and (W).
Most significantly, there is a potential-theoretic problem
corresponding to v. It is also a free-boundary problem for a
(different) harmonic function 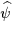 , and the free streamline
does not coincide with the free streamline of , and the free streamline
does not coincide with the free streamline of 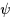 . The problems for . The problems for
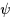 and and 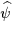 correspond only via duality. However v is
a function of w, and vice versa. correspond only via duality. However v is
a function of w, and vice versa. |
|---|
| |
Une formulation duale des ondes de Stokes |
|---|
| Résumé. |
Le problème des ondes gravitationnelles à la surface
d'un liquide bidimensionnel de profondeur infinie
se ramène à une équation
pour une fonction inconnue 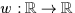 ,qui est non locale, de type quasi-linéaire et qui admet une structure
gradient.
Dans ce travail, nous ne traiterons que des solutions périodiques.
Nous introduisons une équation non locale pour une
fonction périodique inconnue ,qui est non locale, de type quasi-linéaire et qui admet une structure
gradient.
Dans ce travail, nous ne traiterons que des solutions périodiques.
Nous introduisons une équation non locale pour une
fonction périodique inconnue 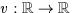 , qui est duale dans le
sens suivant.
On considère un certain système d'équations différentielles du
second ordre
pour deux fonctions inconnues , qui est duale dans le
sens suivant.
On considère un certain système d'équations différentielles du
second ordre
pour deux fonctions inconnues 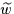 et et 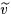 définies sur le
disque unitaire.
En le résolvant partiellement,
on le réduit soit en une équation non locale pour définies sur le
disque unitaire.
En le résolvant partiellement,
on le réduit soit en une équation non locale pour
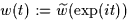 ,soit en une équation non locale pour ,soit en une équation non locale pour
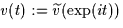 . . |
|---|



Next: About this document ...
Boris Buffoni
11/14/2000